Page 152 - 精细化工2019年第10期

·2118· 精细化工 FINE CHEMICALS 第 36 卷

1.1.3 模型的求解 的稳定值相差也较大，L z =0.05 mm 处的溶氧浓度最
3
3
生物膜增长期显著特点是微生物聚集，生物浓 低值为 0.033 mol/m 是 L z=0.10 mm（0.0098 mol/m ）
度不断增加，传质过程始终发生变化。因此，设定 的 3 倍多，而在 L z=0.15 mm 处溶氧浓度极低为
3
限定初始条件和边界条件如下： 0.001 mol/m ，说明溶解氧所能到达的生物膜厚度是
(,0) 
Cz 0 有限的，也验证了好氧-厌氧复合生物膜结构的合理性。
初始条件： S
C X (,0)z  0 1.1.4.2 渗流速度的影响
C (0, )t  C ; C (L , )t  0 生物膜内部的渗流速度是影响膜内传质的重要
边界条件： S S S z
C X (0,)t  C X ; n C X (L z ,)t  0 参数，其数值与反应器内水力剪切作用和生物膜内的
2
–4
设溶解氧浓度和微生物的浓度分别 C S 和 C X n， 通透性成正比。选择在扩散系数 D 为 2.2×10 m /s、
3
模型中方程的初始条件意义是在 t=0 时，生物膜内 进水溶氧浓度 c 为 0.08 mol/m 的条件下，对设定的
的溶解氧传质尚未开始，因此，C S 浓度为 0，同时 4 个不同渗流速度进行计算，考察了不同渗流速度
生物膜内微生物浓度事先设定为 C X 0；边界条件的 对生物膜内溶解氧分布的影响。图 2a 是在生物膜厚
意义可表述为在 t 时刻生物膜表面即 L z =0 mm 位置 度 L z 为 0.05 mm 处，不同渗流速度下生物膜内溶氧
处基质中溶解氧浓度和微生物浓度分别 C S 和 C X n， 浓度随时间的变化曲线。图中 4 条曲线的变化规律
–2
而在生物膜厚度为 L z =0.25 mm 即生物膜末端 C S 和 略有不同，当渗流速度较大，即 u=3.2 × 10 m/s 时，
C X n 均为 0。 溶氧浓度在前 4 s 内先急剧增大，到达最大值约
3
生物膜数学模型的建立需要设定多种参数 [10] ： 0.064 mol/m 后保持不变；而其他 3 个渗流速度下，
3
液相溶解氧的初始浓度设定为 0.08 mol/m （25 ℃ 溶氧浓度变化规律是在前 7 s 内先急剧增大，但达
时，1 个大气压下水中饱和溶解氧约 8.25 mg/L，即 到最大值后缓慢下降后才保持稳定。这是因为当生
3
0.25 mol/m ）；生物膜厚度为 0.25 mm。扩散系数和 物膜内的渗流速度足够大时，生物膜内溶解氧的传
质途径为对流传质，而在相同时间内通过对流方式
生物膜内液相渗流速度选取不同的数值进行分析计
传递至某一生物膜厚度处的溶解氧浓度越大，其达
算，具体值见表 1。
到最大值所需时间越短，最大值下降至稳定值的幅
1.1.4 溶解氧浓度的影响因素分析
度越小。图 2b 为达到稳定后不同渗流速度下生物膜
1.1.4.1 生物膜厚度的影响
内溶氧浓度随生物膜厚度变化情况。
首先计算了渗流速度 6 mm/s、扩散系数 D 为

3
–4
2
2.2×10 m /s 和进水溶氧浓度 c 为 0.08 mol/m 的条
件下生物膜不同厚度（L z 分别为 0.05、0.10 和
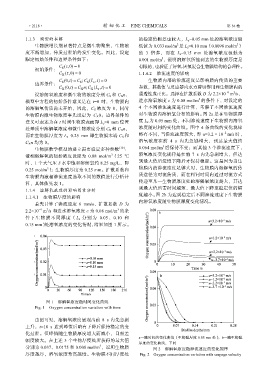
0.15 mm）处溶氧浓度的变化情况，结果如图 1 所示。

图 1 溶解氧浓度随时间变化曲线
Fig. 1 Oxygen concentration variation with time

由图可见，溶解氧浓度呈现出前 8 s 内先急剧
上升，t=10 s 达到峰值后略有下降后保持稳定的变

化过程。但峰值随生物膜厚度增大而减小，且相差
a—随时间的变化曲线（生物膜厚度 0.05 mm 处）；b—随生物膜
幅度较大。在上述 3 个生物厚度处所获得的最大值 厚度的变化曲线，下同
3
分别为 0.037、0.0175 和 0.008 mol/m ，说明生物膜 图 2 溶解氧浓度随渗流速度的变化规律
厚度越厚，溶氧浓度升高越慢。生物膜不同厚度处 Fig. 2 Oxygen concentration variation with seepage velocity