Page 192 - 《精细化工》2020年第1期

·178· 精细化工 FINE CHEMICALS 第 37 卷

系更加紧密，在 SEM 实验中表现为高分子链在空间 型是以 Maxwell 模型为基础推广而来的流变本构方
中更加均匀的分布。这种结构必然导致外界应力在 程，且该模型引入了共旋随流微商 [21] 的概念，使得方
体系中的均匀分布，也是体系高模量的来源。 程具有较高的描述能力。

Cross 方程如式（2）所示：
  
 a     0  （2）
1   m
式中：η a 为剪切黏度，Pas；η 0 为零切黏度，Pas；
η∞为无穷剪切黏度，Pas；λ 为特征时间，s；m 为
–1
非牛顿参数；   为剪切速率，s 。
Jeffrey 共旋随流模型在稳态剪切流场中剪切黏
度的解如式（3）所示：

1    2
 a   0 12 （3）
22
1  1 
式中：λ 1 为第一特征时间，s；λ 2 为第二特征时间，s。
图 4 为不同 M-1 含量下剪切黏度与剪切速率的
关系。表 2 为各方程拟合结果。

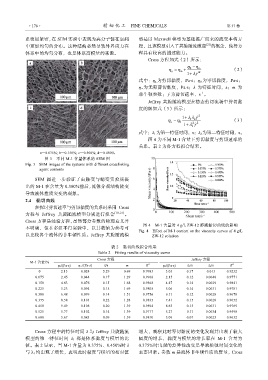
a—0.075%; b—0.150%; c—0.300%; d—0.450%
图 3 不同 M-1 含量体系的 SEM 图
Fig. 3 SEM images of the systems with different crosslinking
agent contents

SEM 图进一步验证了由触变与蠕变实验所提
出的 M-1 在含量为 0.300%前后，流体介观结构转变
导致液体性质突变的现象。
2.4 黏切曲线
在探讨剪切速率与剪切黏度的关系时采用 Cross
方程与 Jeffrey 共旋随流模型分别进行拟合 [18-21] 。

Cross 方程是经验方程，虽然部分参数的物理意义并
图 4 M-1 含量对 4 g/L ZW-12 溶液黏切曲线的影响
不明确，但在多组平行实验中，以其数值为参考可
Fig. 4 Effect of M-1 content on the viscosity curves of 4 g/L
以比较各个流体的非牛顿性质。Jeffrey 共旋随流模 ZW-12 solution

表 2 黏切曲线拟合结果
Table 2 Fitting results of viscosity curve
Cross 方程 J e f f e r y 方程
M-1 含量/% 2 2
η 0/(Pas) η∞/(Pas) λ/s m R η 0/(Pas) λ 1/s λ 2/s R
0 2.13 0.024 5.29 0.69 0.9983 3.03 0.37 0.013 0.9232
0.075 2.45 0.044 0.17 1.29 0.9968 2.15 0.12 0.0040 0.9771
0.150 4.63 0.076 0.15 1.68 0.9868 4.47 0.14 0.0029 0.9841
0.225 5.23 0.094 0.15 1.69 0.9805 5.06 0.14 0.0031 0.9781
0.300 6.48 0.099 0.14 1.51 0.9756 6.11 0.12 0.0028 0.9678
0.375 8.58 0.101 0.22 1.28 0.9835 7.41 0.15 0.0028 0.9652
0.450 9.49 0.108 0.20 1.39 0.9894 8.65 0.15 0.0031 0.9769
0.525 5.77 0.102 0.14 1.39 0.9717 5.27 0.11 0.0034 0.9598
0.600 5.67 0.083 0.09 1.39 0.9810 5.09 0.07 0.0023 0.9632

Cross 方程中的特征时间 λ 与 Jeffrey 共旋随流 增大，观察此时零切黏度的变化发现其出现了较大
模型的第一特征时间 λ 1 都是体系黏度与模量的比 幅度的增长，黏度与模量的增长率在 M-1 含量为
值。表 2 显示，当 M-1 含量为 0.375%、0.450%时 λ 0.375%时出现的差异性改变是导致松弛时间变化的
与 λ 1 均出现了增长，表明此时黏度与模量的相对值 主要因素。参数 m 是流体非牛顿性质的度量，Cross