Page 205 - 《精细化工》2020年第6期

第 6 期 史盼盼，等: 甲基橙在桉木基磁性活性炭上的吸附行为 ·1271·

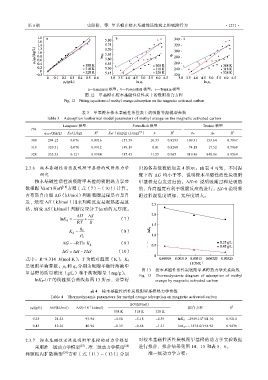
a—Langmuir 模型；b—Freundlich 模型；c—Temkin 模型
图 12 甲基橙在桉木基磁性活性炭上的吸附拟合方程
Fig. 12 Fitting equations of methyl orange adsorption on the magnetic activated carbon

表 3 甲基橙在桉木基磁性活性炭上的吸附等温模型参数
Table 3 Adsorption isothermal model parameters of methyl orange on the magnetic activated carbon
Langmuir 模型 Freundlich 模型 T e m k i n 模型
T/K
2
2
1/n
q max/(mg/g) K L/(L/kg) R K F/〔(mg/g) (L/mg) 〕 n R b T A T R 2
308 294.12 0.076 0.9916 157.39 10.33 0.8293 100.31 153.64 0.7967
318 320.51 0.070 0.9912 149.19 8.01 0.8268 74.18 17.52 0.7968
328 333.33 0.121 0.9984 187.43 11.55 0.965 110.46 848.16 0.9564

2.3.6 桉木基磁性活性炭吸附甲基橙的吸附热力学 出的各参数数值如表 4 所示。由表 4 可知，不同温
研究 度下的 ΔG 均小于零，说明桉木基磁性活性炭吸附
桉木基磁性活性炭吸附甲基橙的吸附热力学参 甲基橙是自发进行的。ΔH>0 说明吸附过程是吸热
数根据 Vant’t Hoff [18] 方程〔式（7）~（10）〕计算。 的，升高温度有利于吸附反应的进行。ΔS>0 说明吸
吉布斯自由能 ΔG（kJ/mol）判断吸附过程是否是自 附过程混乱度增加，无序度增大。
发，焓变 ΔH（kJ/mol）用来判断反应是吸热还是放
热，熵变 ΔS（kJ/mol）判断反应分子运动的无序度。
Δ ΔH S
lnK   （7）
d
RT R
q
K  e （8）
d
 e
Δ RG  T l n K （9）
d
Δ ΔG   Δ H T S （10）

式中：R=8.314 J/(mol·K）；T 为绝对温度（K）；K d

是吸附平衡常数；ρ e 和 q e 分别为吸附平衡时溶液中
图 13 桉木基磁性活性炭吸附甲基橙热力学关系曲线
甲基橙的质量浓度（g/L）和平衡吸附量（mg/g）。
Fig. 13 Thermodynamic diagram of adsorption of methyl
lnK d -1/T 的线性拟合曲线如图 13 所示，计算得 orange by magnetic activated carbon

表 4 桉木基磁性活性炭吸附甲基橙热力学参数
Table 4 Thermodynamic parameters for methyl orange adsorption on magnetic activated carbon
ΔG/(kJ/mol)
–3
ρ 0/(g/L) ΔH/(kJ/mol) ΔS/(×10 kJ/mol) 拟合方程 R 2
308 K 318 K 328 K
0.25 24.52 93.94 –4.50 –5.18 –6.39 lnK d= –2949.1/T+11.30 0.9214
0.45 12.26 40.94 –0.39 –0.68 –1.21 lnK d= – 1474.6/T+4.92 0.9430

2.3.7 桉木基磁性活性炭吸附甲基橙的动力学模型 对桉木基磁性活性炭吸附甲基橙的动力学实验数据
采用准一级动力学模型 [27] 、准二级动力学模型 [28] 进行拟合，拟合结果见图 14、15 和表 5、6。
和颗粒内扩散模型 [29] 方程〔式（11）~（13）〕分别 准一级动力学方程：