Page 208 - 《精细化工》2022年第1期

·198· 精细化工 FINE CHEMICALS 第 39 卷

制，显著特征是更有利于解吸，说明其具有优异的 而吸附等温线主要表现为吸附达平衡时，平衡质量
再生性能；颗粒内扩散模型拟合度虽然很好，但是 浓度 ρ e 和平衡吸附容量 q e 间的数学方程式。为较
其拟合得到的线性均未通过原点，表明在 CSCBC 好描述 CSCBC 吸附 Cr(Ⅵ)过程的热力学现象，分别
吸附 Cr(Ⅵ)过程中，颗粒内扩散并不是唯一控制过 使用 Langmuir 模型、Freundlich 模型和 Dubinin-
程，可能存在其他的控制机制。 Radushkevich（D-R）模型 3 种经典热力学模型对
2.4 吸附等温线 实验数据进行拟合分析 [15] ，模型及相应线性方程见
吸附热力学主要是利用吸附等温线进行描述， 表 4。

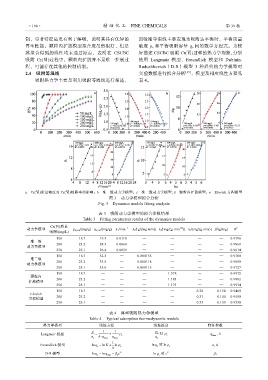
a—Cr(Ⅵ)质量浓度对 Cr(Ⅵ)吸附率的影响；b—准一级动力学模型；c—准二级动力学模型; d—颗粒内扩散模型；e—Elovich 方程模型
图 3 动力学模型拟合分析
Fig. 3 Dynamics models fitting analysis

表 3 吸附动力学模型的拟合参数结果
Table 3 Fitting parameters results of the dynamics models
Cr(Ⅵ)质量
2
1/2
动力学模型 q e,exp/(mg/g) q e,cal/(mg/g) k 1/min –1 k 2/[g/(mg·min)] k t/[mg/(g·min )] v 0/[mg/(g·min)] β/(g/mg) R
吸附/(mg/L)
150 18.7 19.3 0.0110 — — — — 0.9796
准一级
动力学模型 200 23.2 24.3 0.0060 — — — — 0.9869
250 25.1 26.4 0.0059 — — — — 0.9614
150 18.7 32.3 — 0.000155 — — — 0.9700
准二级
200 23.2 33.8 — 0.000118 — — — 0.9850
动力学模型
250 25.1 35.0 — 0.000115 — — — 0.9727
150 18.7 — — — 1.378 — — 0.9972
颗粒内
扩散模型 200 23.2 — — — 1.183 — — 0.9982
250 25.1 — — — 1.173 — — 0.9974
150 18.7 — — — — 0.38 0.158 0.9460
Elovich
方程模型 200 23.2 — — — — 0.31 0.144 0.9550
250 25.1 — — — — 0.33 0.139 0.9330

表 4 典型吸附热力学模型
Table 4 Typical adsorption thermodynamic models
热力学模型 线性方程 线性拟合 特征参数
 1 1  e
Langmuir 模型    对  q max , b
e
e
q e b q  max q max q e
1
Freundlich 模型 ln q  e ln K  ln  ln q 对 ln  n, K
e
e
e
n
2
2
D-R 模型 ln q  e ln q max    ln q 对  β 2
2
e