Page 38 - 201902

·204· 精细化工 FINE CHEMICALS 第 36 卷

表 2 第 26 号机理计算所得参数值
Table 2 Parameters obtained by No.26 mechanism function
β/(℃/min) E a/(kJ/mol) lgA r 2 |(E aoE a)/E ao| |(lgAlgA k)/lgA k|
Achar 5 177.54 13.0197 0.9524 0.0220 0.0829
10 178.63 13.4643 0.9041 0.0160 0.1199
15 182.85 13.8444 0.9114 0.0073 0.1515
20 178.89 13.9848 0.8950 0.0145 0.1632
Average 179.84 13.5783 0.9157 0.0151 0.1294
Coast-Redfern 5 172.32 10.7701 0.9398 0.0507 0.1042
10 181.96 11.4206 0.9590 0.0024 0.0501
15 183.03 11.5570 0.9599 0.0083 0.0387
20 180.47 11.3536 0.9409 0.0058 0.0557
Average 179.45 11.2753 0.9499 0.0168 0.0622

表 3 Friedman 和 Vyazonvkin-Weight 法计算得到的参数值
Table 3 Parameters obtained by Friedman and Vyazonvkin-
Weight methods
Friedman Vyazonvkin-Weight
α/% 2 2
E a/(kJ/mol) r E a/(kJ/mol) r
5 171.76 0.9624 165.70 0.9559
10 178.86 0.9322 169.48 0.9645
15 178.64 0.9187 173.16 0.9434
20 178.69 0.9430 171.36 0.9504
25 182.97 0.8827 175.06 0.9549
30 173.36 0.9276 175.50 0.9454

35 178.39 0.9395 173.58 0.9504
3
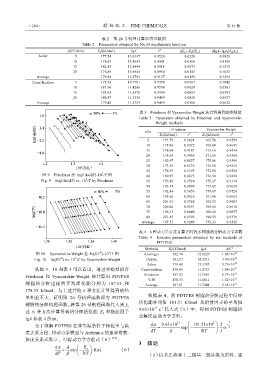
图 9 Friedman 法 ln(β·dα/dT)-10 /T 图 40 180.95 0.8675 176.34 0.9436
3
Fig. 9 ln(β·dα/dT) vs. 10 /T by Friedman 45 176.86 0.9728 175.37 0.9314
50 185.74 0.9090 177.42 0.9624
55 192.84 0.9859 179.67 0.9724
60 192.66 0.9526 181.96 0.9663
65 201.93 0.9528 182.92 0.9683
70 209.06 0.9551 189.04 0.9610
75 196.33 0.8640 188.44 0.9657
80 221.45 0.8392 198.33 0.9376
Average 187.53 0.9249 178.33 0.9545

表 4 6 种动力学方法计算 PDTPES 树脂热分解动力学参数
Table 4 Kinetics parameters obtained by six methods of
PDTPES
–1
Methods E a/(kJ/mol) lgA A/s
2
3
图 10 Vyazonvkin-Weight 法 ln(β/T )-10 /T 图 Kissinger 182.76 12.0227 1.05×10
12
2
3
10
Fig. 10 ln(β/T ) vs. 10 /T by Vyazonvkin-Weight Ozawa 181.53 10.5311 3.40×10
12
Achar 179.48 13.5783 3.79×10
从图 9、10 和表 3 可以看出，通过非模型拟合 Coast-redfern 179.45 11.2753 1.88×10
11
11
Friedman 和 Vyazonvkin-Weight 法计算出 PDTPES Friedman 187.53 11.7581 5.73×10
11
V-W 178.33 11.1811 1.52×10
树脂热分解过程的平均活化能分别为 187.53 和 Average 181.51 11.7244 9.65×10
11
178.33 kJ/mol，与上述其他 4 种方法计算得到的结
根据表 4，将 PDTPES 树脂热分解过程中反应
果相差不大，证明第 26 号机理函数即为 PDTPES
活化能平均值 181.51 kJ/mol 及指前因子的平均值
树脂热分解机理函数。将第 26 号机理函数代入到上
s 代入式（6）中，得到 PDTPES 树脂热
9.65×10 11 –1
述 6 种方法计算得到热分解活化能 E a 和指前因子
分解反应动力学方程：
lgA 如表 4 所示。

为了求解 PDTPES 在非等温条件下转化率与温 d  9.65 10 11 exp   181.51 10   3   2   1 2
d  RT T  3 
度关系方程，将动力学模型与 Arrhenius 的速率常数-  
温度关系式联立，可得动力学方程式（6） [37] ：
d A  E a  3 结论

 exp     f( ) （6）
d   RT T  （1）以苯乙炔和十二烷基三氯硅烷为原料，通