Page 125 - 《精细化工》2021年第10期
P. 125
第 10 期 朱文澄,等: PE 基聚硅氧烷/改性 SiO 2 超疏水薄膜的构筑 ·2055·
进行了 SEM 测试,见图 10。从图 10 可见,在 100 粗糙度。根据 CASSIE 等提出的模型解释 [22] ,材料
mm×100 mm 的 PE 基材表面,复合涂层 S1 表面较为 表面微观结构粗糙度的增加有助于疏水性的提高。
光滑平整,未有凸起,添加了 OTMS-SiO 2 的复合涂
层表面开始出现颗粒状凸起,这是由于纳米尺寸的
OTMS-SiO 2 微观聚集形成了多尺度的微纳结构,增
加了表面粗糙度。随着 OTMS-SiO 2 添加量的进一步
增加,聚集体分布更加密集,粗糙度进一步增加。
而 OTMS-SiO 2 添加量达到 12%时,OTMS-SiO 2 发生
严重团聚,破坏了成膜的连续性,这对复合涂层的
耐磨性会产生不利影响,因此,选取 OTMS-SiO 2 的
最佳添加量为 8%。
为进一步分析复合涂层的表面形貌,采用原子
力显微镜对复合涂层 S1 和 S3 进行了测试,如图 11
所示。由图 11 可以观察到,复合涂层 S1 的平均粗
糙度(R a)为 2.39 nm,根均方粗糙度(R q)为 1.64 nm,
说明表面具有较好的平整性,而复合涂层 S3 的表面
有山峰状不规则小凸起,R a =73.4 nm,R q =91.4 nm,
表面粗糙度远大于 PE 薄膜。这是因为,纳米 SiO 2
a、b—复合涂层 S1;c、d—复合涂层 S3;e、f—复合涂层 S4
微观聚集,涂层表面分布着由纳米尺寸的 SiO 2 团聚
体构成的多层级粗糙结构。同时这种结构有利于截获 图 10 PE 表面不同 OTMS-SiO 2 添加量的复合涂层的
SEM 图
更多的空气,赋予涂层超疏水性能。结合 SEM 的结
Fig. 10 SEM images of PE surface coated by composite
果,证明了疏水改性纳米 SiO 2 确实增加了涂层表面的 coatings with different content of OTMS-SiO 2
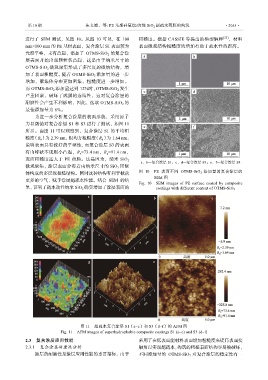
图 11 超疏水复合涂层 S1(a~c)和 S3(d~f)的 AFM 图
Fig. 11 AFM images of superhydrophobic composite coatings S1 (a~c) and S3 (d~f)
2.3 复合涂层应用性能 采用了在低表面能材料表面增加粗糙度来提高表面接
2.3.1 复合涂层耐磨性分析 触角以实现超疏水,构筑的粗糙表面结构容易被破坏,
涂层的耐磨性是涂层应用性能的重要指标,由于 不同添加量的 OTMS-SiO 2 对复合涂层的稳定性有一