Page 100 - 《精细化工》2020年第1期

·86· 精细化工 FINE CHEMICALS 第 37 卷

由图 5 可知，用 Kissinger 极值法、FWO 积分 线性关系，在横坐标–0.51~ –0.22 存在一个最大值，
法两种方法拟合的曲线斜率分别为–6.40、–7.08，带 因此，原子灰选用 BPO-DMA-Co(Ⅱ)固化体系进行
入公式（2）、（3）中得到原子灰在不同升温速率下的 固化属自催化固化模型。
表观活化能，E a1=53.18 kJ/mol、E a2=55.95 kJ/mol，二 2.5.2.2 固化动力学方程的模拟
者算数平均值为 54.57 kJ/mol，与等温测试计算的表 为证明原子灰选用 BPO-DMA-Co(Ⅱ)体系进行
观活化能接近，证明该结果可信度较高。根据 固化符合自催化反应模型，本文将式（6）代入到式
Kissinger 极值法直线的截距，计算指前因子 A 为 （4）中并取对数得到自催化反应模型方程（8）：
–1
7
9.153×10 min 。 d da a E
ln  ln   a  n ln(1 a   ) m a ln ln A （8）
2.5.2 BPO-DMA-Co(Ⅱ)固化机理 d dt R T T 
从文献[23]可知，热固性树脂的固化模型有两 式（8）中的因变量为 ln(da/dT)，自变量为 1/T、
种：n 级反应模型和自催化反应模型。本文采用 ln(1–a)、lna，将 E a 和 A 代入式（8）中，并用线性
Friedman 方程来判定 BPO-DMA-Co(Ⅱ)固化体系的 回归分析就可计算出 BPO-DMA-Co(Ⅱ)固化体系不
固化模型，所用公式如下： 同升温速率条件下的 m、n 值，见表 8 [23] 。

Friedman 方程、n 阶反应模型、自催化反应模
表 8 不同升温速率自催化模型的计算参数
型分别见式 4、5、6。 Table 8 Calculation parameters of auto-catalytic models with
d da a E different heating rates
ln  ln   ln[Af a  ( )] a （4）
d dt T R T  β/(K/min)

n
f ()a  (1 a ) （5） 5 10 15 20 25
f ()a  (1 a a ) n m （6） n 2.66 1.35 1.92 1.14 1.22
m 0.63 0.53 0.55 0.39 0.37
式中：a 为固化度（由 DSC 软件导出），此处 E a(kJ/mol)

–1
和 A(min )是指由 Kissinger 极值法、FWO 积分法计 将表 8 中的计算参数代入到式（8）中，就能得
算所得平均表观活化能和指前因子。 到反应速率 da/dt 与温度 T 的关系拟合曲线，并与实
2.5.2.1 固化模型的确定 验测得的 da/dt 与 T 的关系曲线图进行比较，见图 7。
将式（5）代入式（4）得式（7）：
da E
ln[Af a  ( )] ln  a 
E d Rt T 

ln  da  a  ln A n ln(1 a ) （7）

d RT T 
将 ln[Af(a)]作为因变量，ln(1–a)作为自变量作
图 6。查文献可知，如果曲线是线性关系，那么即
为 n 阶反应模型；如果 ln(1–a)值在–0.51~ –0.22
ln[Af(a)]出现最大值，那么该反应属于自催化反应
模型 [25] 。

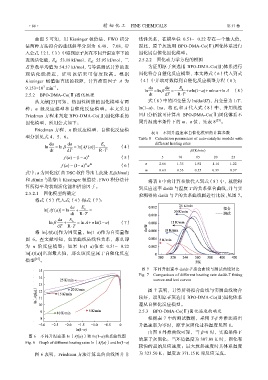
图 7 不同升温速率 da/dt-T 拟合曲线与测试曲线对比
Fig. 7 Comparison of different heating rate da/dt-T fitting
curves and test curves

图 7 表明，计算所得拟合曲线与实测曲线吻合
较好，说明原子灰选用 BPO-DMA-Co(Ⅱ)固化体系
遵从自催化反应模型。
2.5.3 BPO-DMA-Co(Ⅱ)固化温度的确定
根据表 7 中的测试数据，采用 T-β 外推法得出
升温速率为零时，原子灰固化过程温度见图 8。

由图 8 外推曲线可知，当 β=0 时，实验条件下
图 6 不同升温速率 ln〔Af(a)〕和 ln(1–a)关系曲线图
的原子灰固化；当环境温度为 307.88 K 时，固化有
Fig. 6 Graph of different heating rates ln 〔Af(a)〕 and ln(1–a)
较快的起始反应速度；最大放热速度时其体系温度
图 6 表明，Friedman 方法计算出的曲线图并非 为 323.50 K；温度达 371.15 K 时反应完成。