Page 68 - 《精细化工》2021年第9期

·1782· 精细化工 FINE CHEMICALS 第 38 卷

2.2 电磁性能分析 介电频散现象。在所测频段内，按 ε′和 ε″大小排序
图 4 为 3 种吸波剂与石蜡以质量比 1∶4 均匀混 均为 S-PG>L-PG>H-PG，与表 1 所示 3 种粉体全粉
合所测得的电磁参数。 压片所测电导率的变化规律及 SEM 形貌分析结果一
致，这表明 S-PG 和 L-PG 具有更高的介电存储和损
+ 2–
耗能力，原因在于 H 浓度相同，对负离子为 SO 4
–
和大分子樟脑磺酸根（CSA ）可通过静电吸引或氢
键等相互作用进一步加强 PANI 链间及 PANI 与 GO
间的载流子传输 [22] 。介电损耗正切（tanδ ε =ε″/ε′）表
示电磁能量损失部分与储存部分的比值，常用于衡
量吸波材料的介电损耗性能。图 4c 为 3 种样品的
2–
tanδ ε 随频率变化曲线，表明对负离子为 SO 4 时氧化
石墨烯/聚苯胺复合物的介电损耗性能最高，对负离
–
子为 CSA 时氧化石墨烯/聚苯胺复合物介电损耗性
能较低。图 4d 中 3 种样品的相对磁导率实部 μ′随频
率变化在 1.0 附近波动，虚部 μ″在 0 附近波动，这
与石蜡基体的数值接近，表明 3 种样品的磁损耗贡
献很小。

表 1 H-PG、L-PG 和 S-PG 全粉的电导率
Table 1 Conductivity of H-PG, L-PG and S-PG
样品 电导率/(S/cm)
H-PG 0.621
L-PG 4.553
S-PG 5.500

根据德拜偶极子弛豫模型 [23] ，可以推导出相对
介电常数虚部 ε″与实部 ε′间的关系，如式（3）所示：
  2      2      2 （3）
   s
式中：ε∞为频率无限大时的相对介电常数，ε s 为静态
频率下的相对介电常数。ε″-ε′曲线应为半圆形，命
名为 Cole-Cole 圆，每个半圆对应一个德拜弛豫过程。
H-PG、L-PG 和 S-PG 的 Cole-Cole 曲线如图 5
所示。

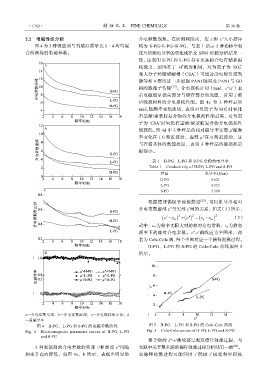
a—介电常数实部；b—介电常数虚部；c—介电损耗角正切；d
—复磁导率
图 4 H-PG、L-PG 和 S-PG 的电磁参数曲线 图 5 H-PG、L-PG 和 S-PG 的 Cole-Cole 曲线
Fig. 4 Electromagnetic parameter curves of H-PG, L-PG Fig. 5 Cole-Cole curves of H-PG, L-PG and S-PG
and S-PG
复合物的 ε″-ε′曲线都呈现双德拜弛豫过程，与
3 种吸波剂的介电常数的实部 ε′和虚部 ε″均随 文献中关于聚苯胺的德拜弛豫过程分析结果一致 [24] 。
频率升高而降低，如图 4a、b 所示，表现出明显的 双德拜弛豫过程可能归因于偶极子极化和界面极