Page 82 - 201906

·1088· 精细化工 FINE CHEMICALS 第 36 卷

2.6.2 回归分析与方差分析
利用 Design-Expert 8.0.6 软件对表 3 数据建立
反应时间（A）、n(苯甲醛)∶n(2-乙酰呋喃)（B）、氢
氧化钾质量分数（C）三因素对产物 FPPO 产率影响
的多元二次响应面回归方程为：
Y=62.78 – 0.42A + 0.9B + 0.8 C – 0.075 AB +
2
2
2
0.12 AC + 0.075 BC – 2.3 A – 4.45 B – 1.45 C
该模型的回归系数和方差分析的显著性检验见
表 4。

图 8 催化剂用量对 FPPO 产率的影响 表 2 响应面实验因素水平表
Fig. 8 Effect of catalyst dosage on the yield of FPPO Table 2 Factors and levels of the response surface design
A：反应 B：n (苯甲醛)∶ C：氢氧化钾质
2.5.6 KOH 质量分数对 FPPO 产率的影响 水平 时间/h n (2-乙酰呋喃) 量分数/%
在 n(KOH)∶n(2-乙酰呋喃)=0.4:1 条件下，考察 –1 0.5 1.3∶1 4.0
0 1.0 1.4∶1 5.0
不同质量分数的 KOH 水溶液对 FPPO 产率的影响，
1 1.5 1.6∶1 7.5
结果见图 9。
表 3 实验设计方案与结果
Table 3 Design and results of experiment
实验号 A B C 产率/%
1 0 1 1 58.5
2 0 0 0 62.8
3 0 0 0 63.2
4 –1 1 0 57.7
5 0 0 0 62.6
6 1 –1 0 54.5
7 –1 0 1 60.0
8 –1 0 –1 58.8

9 0 0 0 62.0
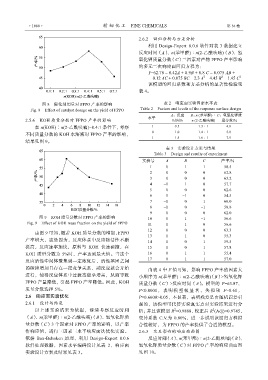
图 9 KOH 质量分数对 FPPO 产率的影响 10 0 1 –1 56.6
Fig. 9 Effect of KOH mass fraction on the yield of FPPO 11 1 1 0 56.6

由图 9 可知，随着 KOH 质量分数的增加，FPPO 12 0 0 0 63.3
13 –1 –1 0 55.3
产率增大，这是因为，反应体系中反应物活性不断 14 1 0 1 59.5
提高，反应速率加快，原料与 KOH 快速碰撞，在 15 1 0 –1 57.8
KOH 质量分数为 5%时，产率达到最大值。当这个 16 0 –1 –1 55.4
17 0 –1 1 57.0
反应活性中间体聚集到一定浓度后，活性基团之间

的碰撞增加且存在一定竞争关系，副反应就会开始 由表 4 中 F 值可知，影响 FPPO 产率的因素大
进行，使得反应体系中过渡态能垒增高，从而导致 小顺序为 n(苯甲醛)∶n(2-乙酰呋喃)（B）>氢氧化钾
FPPO 产量降低，引起 FPPO 产率降低。因此，KOH 质量分数（C）>反应时间（A）。模型的 F=63.87，

质量分数选择 5%。 P<0.0001 ， 表 明 模 型极显 著， 失拟项 F=0.61 ，
2.6 响应面实验优化 P=0.6608>0.05，不显著，表明残差是由随机误差引
2.6.1 设计与结果 起的，该模型可代替实验真实点对实验结果进行分
以上述实验结果为依据，继续考察反应时间 析；并且该模型 R =0.9888，校正后 R (Adj)=0.9745，
2
2
（A）、n(苯甲醛)∶n(2-乙酰呋喃)（B）、氢氧化钾质 变异系数 C.V.为 0.80%，进一步说明该回归方程拟
量分数（C）3 个因素对 FPPO 产率的影响，以产率 合性较好，为 FPPO 的产率提供了合适的模型。
作响应值，进行三因素三水平响应面法优化实验。 2.6.3 交互影响的响应曲面图
依据 Box-Behnken 原理，利用 Design-Expert 8.0.6 反应时间（A）、n(苯甲醛)∶n(2-乙酰呋喃)（B）、
软件处理数据，因素水平编码设计见表 2，响应面 氢氧化钾质量分数（C）对 FPPO 产率的响应曲面图
实验设计方案及结果见表 3。 见图 10。