Page 123 - 《精细化工》2021年第5期

第 5 期 朱雅雯，等: 金柑结合多酚的制备及其对 RAW 264.7 巨噬细胞免疫调节活性 ·977·

略有差异。 为 B>C>A。实验选用的模型（p=0.0002）极显著，
失拟项（p>0.05）不显著，表明该模型用于优化提
表 2 Box-Behnken 实验设计及结果
Table 2 Box-Benhnken experimental design and results 取金柑 NEPP 是可行的。信噪比为 28.773 较高，说
明该模型可以用于预测金柑 NEPP 含量，而模型校
A 脉冲数 B 场强 C 液料比 NEPP 含量 2
实验号 /(mg GAE/g 正判定系数 R Adj =0.9849，表明 98.49%的数据可以用
/次 /(kV/cm) /(L∶g)
DW) 2
此方程解释。判定系数 R =0.9946，说明模型拟合程
1 350 12 0.25∶1 1.58431
度良好，可以使用该模型分析和预测提取效果。
2 450 12 0.38∶1 1.57352
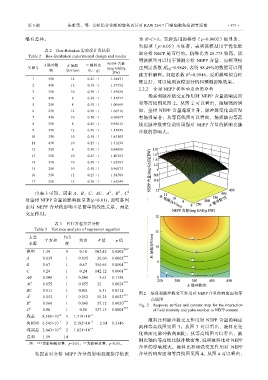
2.2.2 金柑 NEPP 提取响应面图分析
3 350 10 0.38∶1 1.59834
场强和脉冲数交互作用对 NEPP 含量的响应面
4 450 8 0.38∶1 1.17677
5 250 8 0.38∶1 1.00669 和等高线图见图 2。从图 2 可以看出，随场强的增
6 250 12 0.38∶1 1.66516 加，金柑 NEPP 含量逐渐上升，脉冲数变化曲面没
7 450 10 0.50∶1 0.90097 有场强显著；从等高线图可以看出，场强轴向等高
8 350 8 0.25∶1 0.95613 线比脉冲数密集说明场强对 NEPP 含量的影响比脉
9 350 12 0.50∶1 1.15839 冲数的影响大。
10 350 10 0.38∶1 1.63185

11 450 10 0.25∶1 1.51234
12 350 8 0.50∶1 0.84008
13 250 10 0.25∶1 1.10323
14 350 10 0.38∶1 1.62387
15 250 10 0.50∶1 0.96073
16 350 12 0.25∶1 1.58589
17 250 12 0.50∶1 1.65244

2
2
由表 3 可知，因素 A、B、C、AC、A 、B 、C 2
对金柑 NEPP 含量的影响极显著(p<0.01)，说明各因
素对 NEPP 含量的影响不是简单的线性关系，而是
交互作用。

表 3 回归方程方差分析
Table 3 Variance analysis of regression equation
方差 自由
来源 平方和 度 均方 F 值 p 值
模型 1.59 9 0.18 102.42 0.0002 ***
A 0.035 1 0.035 20.60 0.0062 ***
B 0.67 1 0.67 354.65 0.0001 ***
C 0.24 1 0.24 142.12 0.0001 ***
AB 0.006 1 0.006 3.61 0.1158
AC 0.055 1 0.055 32 0.0024 ***

BC 0.011 1 0.011 6.51 0.0512 图 2 场强和脉冲数交互作用对 NEPP 含量的响应面和等
2
A 0.052 1 0.052 50.25 0.0027 *** 高线图
2
B 0.060 1 0.060 35.12 0.0020 *** Fig. 2 Response surface and contour map for the interaction
2
C 0.56 1 0.56 327.13 0.0001 *** of field intensity and pulse number to NEPP content
–3
残差 8.588×10 5 1.718×10 –3 液料比和脉冲数交互作用对 NEPP 含量的响应
–3
失拟项 6.545×10 3 2.182×10 –3 2.14 0.3346
面和等高线图见图 3。从图 3 可以看出，液料比变
–3
纯误差 2.043×10 2 1.021×10 –3
化曲面比脉冲数曲面陡；从等高线图可以看出，液
总和 1.59 14
料比轴向等高线比脉冲数密集，说明液料比对 NEPP
注：***为影响极显著，p<0.01；**为影响显著，p<0.05。
含量的影响较大。液料比和场强交互作用对 NEPP
各因素对金柑 NEPP 含量的影响程度排序依次 含量的响应面和等高线图见图 4。从图 4 可以看出，